
To Infinity… and Beyond!
I don’t remember exactly when I learned the concept of infinity, but at some point in childhood I was using it as a trump card in arguments with my sister. We’d volley along the lines of:
“I have seven beads!”
“Well, I have twelve beads!”
“I have infinity beads!”
(Drops mic.)
Infinity seems like an abstract mathematical concept, and I suppose it is. But one application of infinity is integral to many aspects of everyday human cognition, including language, music, and problem solving. It’s called recursion, and children begin to grasp it around age 9, according to a fascinating study published in the October issue of Cognition. What’s more, a child’s understanding of recursion in pictures is tightly linked to her understanding of grammar.
People define recursion in different ways, all of which are pretty opaque. Wikipedia calls it “the process of repeating items in a self-similar way.” Cognitive scientist Steven Pinker described it as “a procedure that calls itself,” or “a constituent that contains a constituent of the same kind.” Luckily the Wikipedia entry begins with an image that conveys recursion — and its connection to infinity — far more clearly than any technical definition:

Recursion, long studied by mathematicians and computer scientists, became a big topic in cognitive science thanks to the linguist Noam Chomsky, who has written extensively about the importance of recursion in language. My favorite example of linguistic recursion comes from a song* I learned at summer camp:
This is the song that never ends,
Yes it goes on and on my friends.
Some people started singing it, not knowing what it was,
And they’ll continue singing it forever just because…
(Repeat.)
A more complex example of linguistic recursion is a compound noun, such as “student film committee,” note the authors of the new Cognition paper. In order to understand the compound noun’s meaning, you only have to learn one rule: that each word is a descriptor of the words to its right. (What type of committee? A film committee. What type of film? Student films.) This rule could, like the camp song, go on and on: A…particle physics graduate student film committee, say.
“Recursion is interesting and unique,” the authors write, “because it allows the generation of multiple hierarchical levels with a single rule.”
So if recursion is such an important part of the way we think, it makes sense to ask when and how it develops. The new study focused on the development of a visual form of recursion that, unlike language, most children aren’t familiar with: fractals.
Here’s how to make a fractal: Begin with a shape, apply a single rule to it, then repeat that rule. The ‘Sierpinski carpet,’ for example, starts with a square and applies the rule of surrounding it with eight other squares. Then it repeats the rule on each of those new squares:

In the study, the researchers showed fractals to 52 children: 26 who were in second grade (7-8 years old) and 26 who were in fourth grade (9-10 years old).
The kids saw a series of three images that progressively illustrated the fractal pattern (see top row in picture below). Then they were shown two new images (bottom row) and asked to choose the one that continued the pattern.

It’s kind of a tough task, right? But the study found that the fourth graders did pretty well, with 70 percent of them choosing correct answers at a rate higher than chance. In contrast, only 27 percent of the second graders performed better than chance.
What’s more, for children in both groups, their scores on a standardized grammar test predicted how well they did on the fractal task. (And this relationship held even when general intelligence was taken into account.) These results suggest, the authors write, that the brain uses a common system for processing hierarchical relationships, regardless of whether they are visual or linguistic. And that this system comes online sometime between second and fourth grade.
This study doesn’t address the nature of the cognitive machinery driving these skills. But some of the same authors published a brain-imaging study that does. As reported in this month’s issue of NeuroImage, the researchers scanned the brains of 40 adults while they performed the same fractal task that the kids did in the other study. The participants also performed a second task in which they had to find geometric patterns, but the patterns did not require recursion. Here’s an example:
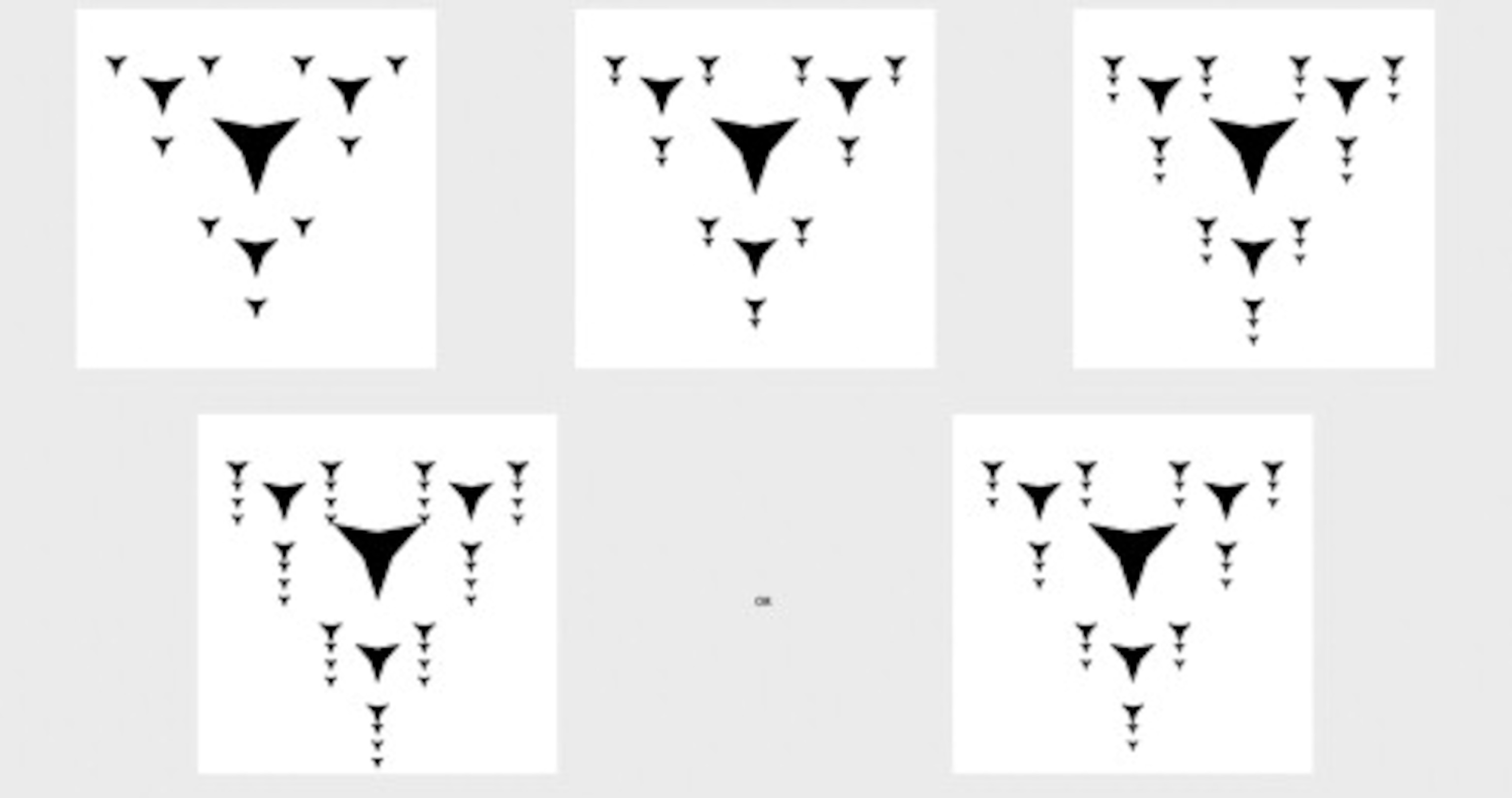
For this latter task, participants must add elements to a pre-existing hierarchy, whereas with the recursive task they’re adding new levels to the hierarchy.
It turns out that we use distinct (and widely distributed) brain networks to process fractals, including brain regions known to be involved in the integration of spatial and semantic information.
I wanted to end this post with some kind of witty one-liner about recursion, something to the tune of, “To understand what this all means, the researchers will need to really think about what it all means.” But that’s pretty lame joke. Google “recursion” and you’ll see a better one.
—
*I wondered whether this song really was recursive, as it doesn’t really have hierarchal nesting. Happily some geeks have weighed in on this very question.
